

A fractal is an object that exhibits self-similar and repeating patterns that display at every scale.
We are interested in studying properties of fractals, such as perimeter and area. Fractals also provide a visualization for recursions, often studied in mathematics and computer science. A recursion is simple a repeated application of some definition or procedure.
The Sierpinski Triangle fractal is constructed in the following manner:
Let's assume that the side lengths of a given equilateral triangle are 1 unit.
Then \[ P_0 = 1 + 1 + 1 = 3 \]
Now consider the first iteration. We now have 3 triangles with side length 1/2.
\[ P_1 = 3(triangles) \cdot 3(sides) \cdot \frac{1}{2}(side length) = \frac{9}{2} \]
The second iteration...
\[ P_2 = 9(triangles) \cdot 3(sides) \cdot \frac{1}{4}(side length) = \frac{27}{4} \]
and so on...
\[ P_3 = 27(triangles) \cdot 3(sides) \cdot \frac{1}{8}(side length) = \frac{81}{8} \\
P_4 = 81(triangles) \cdot 3(sides) \cdot \frac{1}{16}(side length) = \frac{243}{16}\\
P_5 = 243(triangles) \cdot 3(sides) \cdot \frac{1}{32}(side length) = \frac{729}{32}\]
Now let's consider the sequence of perimeters through the first five iterations.
\[ \left \{3, \frac{9}{2}, \frac{27}{4}, \frac{81}{8}, \frac{243}{16}, \frac{729}{32} \right \} \\
= \left \{\frac{3}{1}, \frac{9}{2}, \frac{27}{4}, \frac{81}{8}, \frac{243}{16}, \frac{729}{32} \right \} \\
= \left \{\frac{3^{1}}{2^{0}}, \frac{3^{2}}{2^{1}}, \frac{3^{3}}{2^{2}}, \frac{3^{4}}{2^{3}}, \frac{3^{5}}{2^{4}}, \frac{3^{6}}{2^{5}} \right \}\]
Notice that the sequence is geometric with the following common ratio:
\[ \frac{3^{n+1}}{2^{n}} \]
Since fractals are infinite, we can find the true perimeter of the Sierpinski triangle by finding the limit as it approaches infinity. \[ \lim_{n \to \infty} \frac{3^{n+1}}{2^{n}} = \infty\]
For sake of simplicity, let's assume we have an equilateral triangle whose area is 1 unit.
Then \[ A_0 = 1 \]
If we perform the first iteration, we are constructing four EQUIVALENT triangles and removing the central one.
Thus \[ A_1 = 1 - \frac{1}{4} = \frac{3}{4} \]
If we continue this trend, we are taking three fourths of the area of each triangle of each iteration. Therefore, we are left with the following areas:
\[ A_2 = \frac{3}{4}(current\,area) \cdot \frac{3}{4}(how\,much\,of\,the\,area\,we\,want) = \frac{9}{16} \\
A_3 = \frac{9}{16}(current\,area) \cdot \frac{3}{4}(how\,much\,of\,the\,area\,we\,want) = \frac{27}{64} \\
A_4 = \frac{27}{64}(current\,area) \cdot \frac{3}{4}(how\,much\,of\,the\,area\,we\,want) = \frac{81}{256} \\
A_5 = \frac{81}{256}(current\,area) \cdot \frac{3}{4}(how\,much\,of\,the\,area\,we\,want) = \frac{243}{1024}\]
As we did with the perimeter, lets take a look at the sequence of areas from the first five iterations.
\[ \left \{1, \frac{3}{4}, \frac{9}{16}, \frac{27}{64}, \frac{81}{256}, \frac{243}{1024} \right \} \\
= \left \{\frac{1}{1}, \frac{3}{4}, \frac{9}{16}, \frac{27}{64}, \frac{81}{256}, \frac{243}{1024} \right \} \\
= \left \{\frac{3^{0}}{4^{0}}, \frac{3^{1}}{4^{1}}, \frac{3^{2}}{4^{2}}, \frac{3^{3}}{4^{3}}, \frac{3^{4}}{4^{4}}, \frac{3^{5}}{4^{5}} \right \} \]
Which we can see gives us a geometric series with the following common ratio:
\[ \frac{3^{n}}{4^{n}} \]
As with the perimeter, in order to find the true area of a fractal, we must find the limit of the ratio as it approaches inifity.
\[ \lim_{n \to \infty} \frac{3^{n}}{4^{n}} = 0\]

The Pythagoras Tree fractal is constructed in the following manner:
Let's assume we have a square with side lengths of √2 units.
So \[ A_0 = \sqrt{2} \cdot \sqrt{2} = \sqrt{2}^{2} = 2 \]
In order for one side to be the hypotenuse of a 45-45-90 triangle, we know the legs must be of length 1.
Thus, the first iteration of the Pythagoras Tree gives us two squares with side length of 1.
Notice that \[ A_1 = A_0 + (2 \cdot 1^{2}) = 2 + 2 = 4 \]
If we follow the same steps in the second iteration, for the hypotenuse to be 1 unit, the legs must be of length √1/2.
\[ A_2 = A_0 + A_1 + (4 \cdot \left(\sqrt{\frac{1}{2}}\right)^{2}) \\= 2 + 2 + (4 \cdot \frac{1}{2}) \\= 2 + 2 + 2 \\= 6\]
We can see that the sum of the areas of the same sized squares are equal to the original square's area.
Thus, a generalized formula: \[ A_n = 2(n+1) \]
Even more general for side length s: \[ A_n = s^{2}(n+1) \]
In order to find the true area of the fractal in our example, we need to find the limit of this formula as it approaches infinity.
\[ \lim_{n \to \infty} 2(n+1) = \infty \]
HOWEVER, we have not shown that the area of the fractal diverges. We have shown that the sum of the areas of each square diverges. What we have failed to consider is the overlap that occurs beginning in the fifth iteration. Consider the eleventh iteration shown below.

(Lawrence H. Riddle)
Notice the overlap in the tree. Also notice a more defined tree shape is being formed. While the exact area of this fractal is unkown, we can see that it does in fact converge to some finite value.
(Wikipedia)
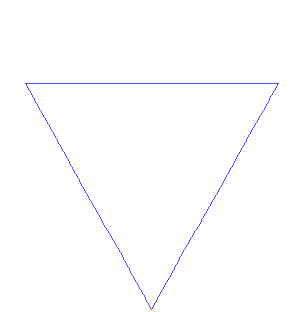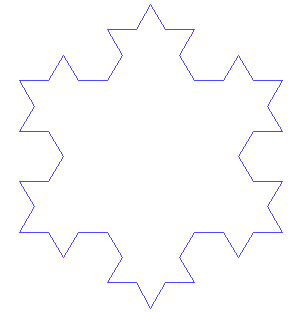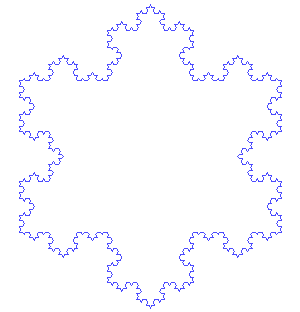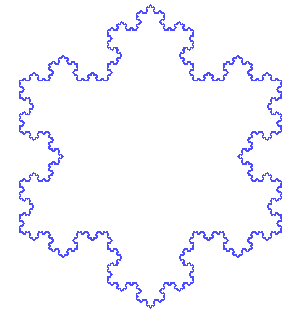
The Koch Snowflake fractal is constructed in the following manner:
Let's assume the side length of an equilateral triangle is one unit.
Then the side length \[S_{0} = 1\] and number of sides \[N_{0} = 3\] give us perimeter \[ P_{0} = N_{0} \cdot S_{0} = 3(sides) \cdot 1(sidelength) = 3 \]
Notice that after each iteration, the side length becomes a third of the value as the previous iteration. Consider the side length after each iteration is as follows when s is the side length of the original equilateral triangle. \[S_{n} = \frac{S_{n-1}}{3} = \frac{s}{3^{n}} \]
We can also see a pattern for calculating the number of sides in each iteration. Each original side increases by a factor of four after each iteration.
\[N_{n} = 3 \cdot 4^{n} \]
Hence we can generalize the perimeter for any iteration by the following.
\[P_{n} = N_{n} \cdot S_{n} = 3 \cdot 4^{n} \cdot \frac{s}{3^{n}} = 3 \cdot s \cdot \left( \frac{4}{3}\right) ^{n}\]
Of course, to truly find the perimeter of the Koch snowflake we must take its limit as it approaches inifity.
\[ \lim_{n \to \infty} 3 \cdot s \cdot \left( \frac{4}{3}\right) ^{n} = \infty \]
When calculating the area of the Koch snowflake, consider an equilateral triangle is added to each side of the iteration. We can represent this addition to find the total number of triangles below.
\[ T_{n} = 3 \cdot 4^{n - 1} = \frac{3}{4} \cdot 4^{n} \]
Consider an as the area of each added triangle in the nth iteration. By this logic notice a0 is the area of the original triangle.
\[ a_{n} = \frac{a_{n-1}}{9} = \frac{a_{0}}{9^{n}} \]
Let bn represent the total area of the iteration.
\[b_{n} = T_{n} \cdot a_{n} = \frac{3}{4} \cdot \left( \frac{4}{9} \right) ^{n} \cdot a_{0} \]
Now we want to see the total area of the snowflake after n iterations. This is modelled below.
\[ A_{n} = a_{0} + \sum^{n}_{k =1} b_{k} \\
= a_{0} \left( 1 + \frac{3}{4} \sum^{n}_{k=1} \left(\frac{4}{9} \right) ^{k} \right) \\
= a_{0} \left( 1 + \frac{1}{3} \sum^{n-1}_{k=0} \left( \frac{4}{9} \right) ^{k} \right) \\
= a_{0} \left( 1 + \frac{3}{5} \left( 1 - \left( \frac{4}{9} \right) ^{n} \right) \right) \\
= \frac{a_{0}}{5} \left( 8 - 3 \left( \frac{4}{9} \right) ^{n} \right) \]
By taking the limit of the area, we get the following:
\[ \lim_{n \to \infty} A_{n} = \lim_{n \to \infty} \frac{a_{0}}{5} \left( 8 - 3 \left( \frac{4}{9} \right) ^{n} \right) \\
= \frac{8}{5} \cdot a_{0}\]
Hence the area of the Koch snowflake is 8⁄5 of the area of the given triangle.
